Dr. Sam Mattheus (29) bereikt baanbrekend resultaat in de Ramsey-theorie. Hij combineerde zijn kennis over de eindige meetkunde met de klassieke grafentheorie en loste niet alleen een decennia oud probleem op, maar biedt een innoverend alternatief voor de huidige aanpak van Ramsey-problemen. “Ook om andere Ramsey-getallen te berekenen, kan de eindige meetkunde hopelijk oplossingen bieden”, zegt Mattheus.
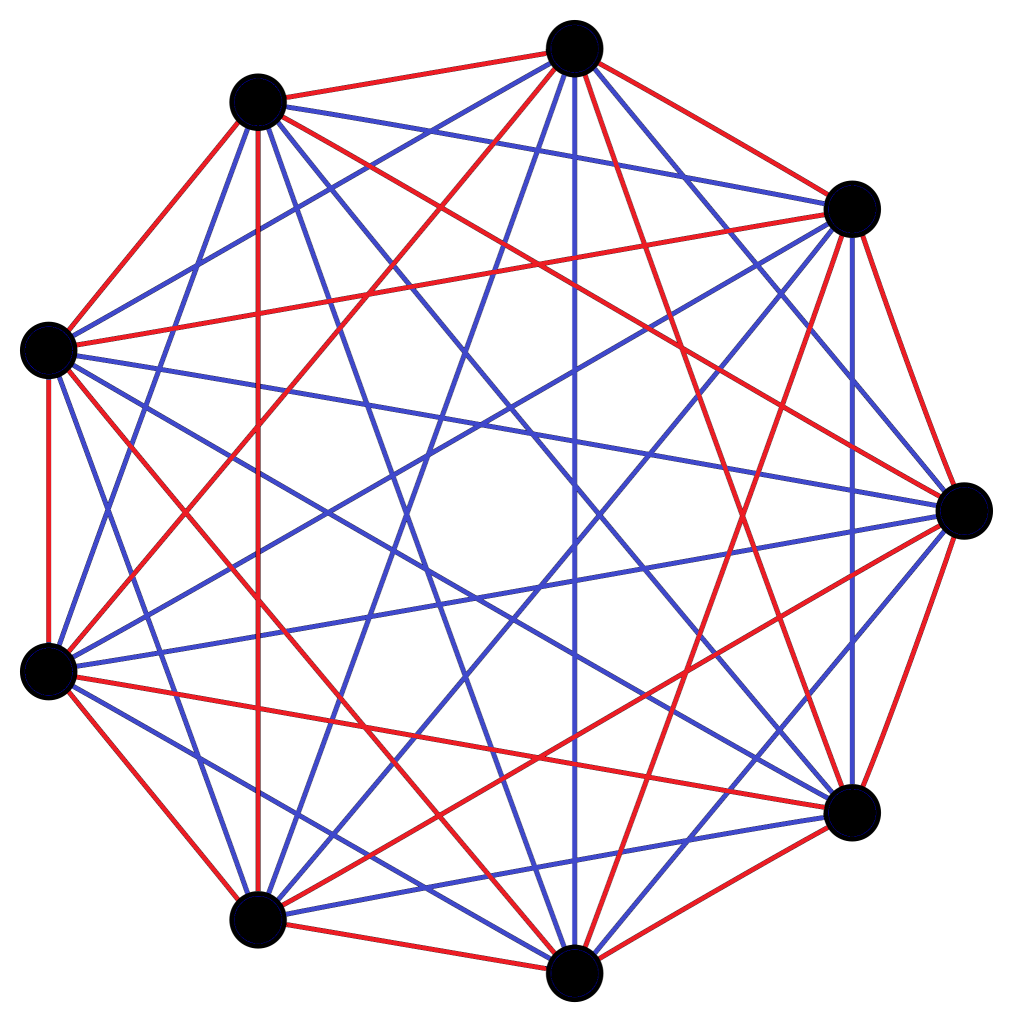
Het vraagstuk dat Mattheus oploste, kadert binnen de zogenaamde Ramsey-getallen. Dat zijn fundamentele grootheden die de grenzen van mogelijke wanorde weergeven. Ze zijn vooral notoir moeilijk te berekenen.
De grafentheorie is de klassieke manier om Ramsey-getallen te berekenen, Mattheus voegde daar zijn eigen kennis aan toe. Met de Hermitische kromme, een bekend object uit de eindige meetkunde, vond Mattheus de sleutel om het probleem r(4,t) op te lossen. “Het was een kwestie van twee domeinen, de eindige meetkunde en de grafentheorie, te combineren”, zegt Mattheus. “De nodige kennis bestond al, maar de ideeën waren nog niet bij elkaar gebracht. Het draaide om the right place and the right time. We pleiten zo eigenlijk voor meer kruisbestuiving binnen de wiskunde. Ook om andere Ramsey-getallen te berekenen, kan de eindige meetkunde hopelijk oplossingen bieden.”
Op de site van de VUB een interview en een heldere uitleg uitleg over Ramsey-getallen. Ramsey-problemen onderzoeken hoelang het duurt voor er in wanorde patronen ontstaan.